Before we can talk about the subject of this article, we must define some
terms:
So, any integer greater than one is either prime or composite. For example, 4= 2*2 and 6= 2*3 are composite, while 3 and 5 are prime.
For example, the proper factors of 6 are 1, 2, and 3.
Informally, a highly-composite integer is one that has many proper factors. One can think of prime numbers, each of which has only a single proper factor—the number 1—and highly-composite numbers as representing two extremes, with most integers lying somewhere in between.
Despite the success of the metric system, highly-composite integers continue to be used for divisions of time and angle. There are 60 seconds in a minute and 60 minutes in an hour, 12 months in a year, 12 hours in a half day, 12 months in a year, and 360 degrees in a circle. In the English system of units, there are 12 inches in a foot, 36 inches in a yard, and 144 (of something) in a gross. The French revolutionaries briefly instituted a calendar with 10 months per year, but it never caught on.
In the Jewish and Christian traditions, the numbers 12 and 120 are associated with completeness. Jacob's 12 sons gave rise to the 12 tribes of Israel. In Genesis 6:3, G-d says: My spirit shall not abide in man forever, for that he also is flesh; therefore shall his days be a hundred and twenty years.
In some folklore traditions, certain numbers that are one greater than a highly-composite number are either very lucky (e.g., 7) or very unlucky (e.g., 13). The number 19, which is one greater than the moderately-composite number 18, has special significance in the Baha'i religion.
Efficient algorithms for calculating the discrete Fourier transform—an important tool in digital signal processing—exist when the length of the data sequence is a product of many small primes. (The ideal situation is that in which the length is a power of 2).
Suppose that we wish to assign a numerical measure of compositeness to any integer. It is not obvious how this should be done. One cannot simply use the number of factors or the sum of the factors as a measure of compositeness because these favor larger integers over smaller ones. (Such measures are meaningful only when one compares sufficiently large numbers of comparable magnitude).
Figures 1 and 2 plot the numbers of proper factors and the sums of the
proper factors, respectively, for each integer from 3 to 360. The blue line on
each plot represents the envelope of the data. Intuitively, this is a
curve that follows the "ups" but not the "downs" of the data. A more formal
definition of the term envelope will be given shortly.
From the figures, it is clear that neither the number of proper factors nor the sum of the proper factors is a good measure of compositeness because both of these favor large integers over small ones.
If one ignores the jagged behavior of the envelope line in Figure 2 and considers only the large-scale behavior, one might guess that one can compensate for the growth by normalizing each sum of proper factors by the number n. Define
_eq.png)
This function is plotted in Figure 3 below. (The green line will be
explained shortly).
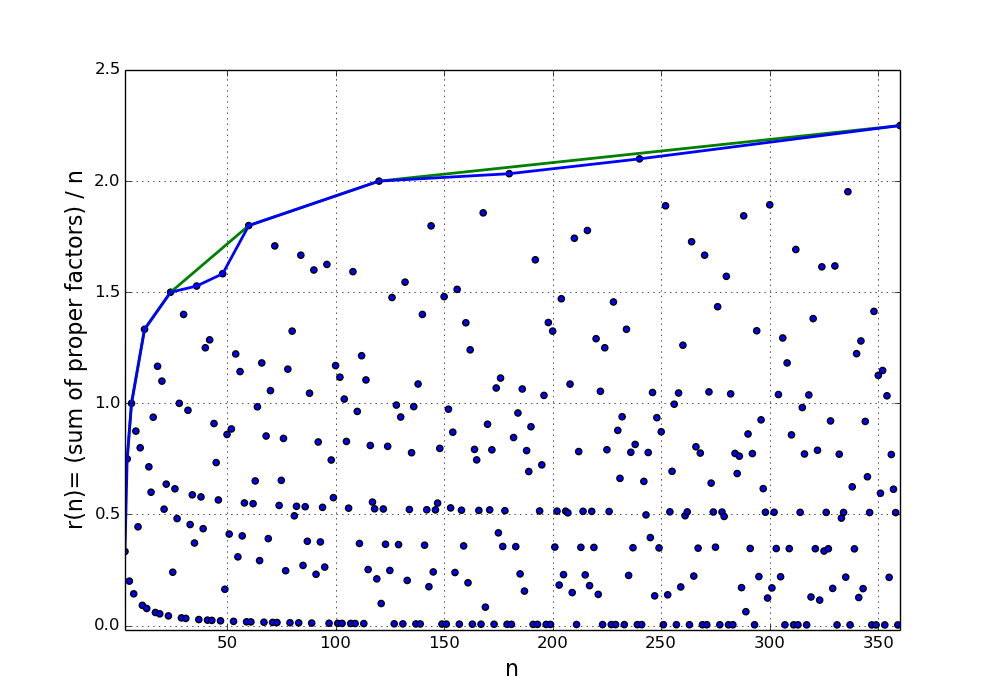
Figure 3 suggests that the normalization is not completely compensating for the growth. But of course, one cannot prove anything with a graph.
We can easily prove that the normalized sum r(n) diverges to infinity, i.e.,
that it will exceed any specified value for some corresponding finite value of
n. To do this, consider numbers n of the form
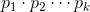, where 
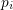is the ith prime.
Because n is the product of the first k primes, the sum of its proper factors can be decomposed as follows:
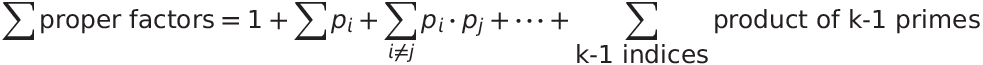
In the expression above, let's discard all of the sums except the final one and then apply the normalization by n. The result is the following:
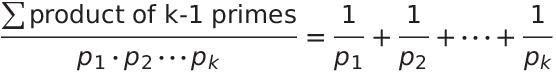
The expression on the right-hand side is the sum of reciprocals of the first k primes. By a theorem of Euler, this sum diverges to infinity. The normalized sum of proper factors overbounds the sum of reciprocals of primes (recall that we discarded some of the component sums), and thus it also diverges.
Because the three simple measures of compositeness discussed above all tend to produce larger values for larger integers, none of them is satisfactory. There are at least two possible remedies:
Use a better normalization. A normalization that correctly compensates for the asymptotic behavior of the sum of the proper factors is available; see the Wikipedia article on the divisor function. Unfortunately, this normalization does not work well for small integers because the convergence to the asymptotic law is quite slow.
Compare the normalized sum of proper factors r(n) against an envelope of r(n), classifying n as highly-composite if the ratio of the two exceeds some threshold.
I've followed the second of these two approaches. In general, the threshold can be an arbitrary function of n, but I've chosen the simplest function, which is a constant. (A non-constant function could be used to control how the density of highly-composite numbers varies with n).
Possible ways to define an envelope of r(n) include the following:
a piecewise-linear function that has the minimum possible value for all n subject to the requirements that the function is monotone increasing and never less than r(n).
the convex hull of the function r(n). (More precisely, this is the upper boundary of the convex hull). This definition of the envelope produces the green line shown in Figure 3. Note that the blue and green lines both correspond to piecewise-linear functions, but the convex hull has the nice property that the slopes of the segments decrease monotonically.
a smooth curve such as a quadratic spline that passes through all of the points (n, r(n)) such that r(n) > r(m) for all m < n (i.e., through all of the points where segments of the blue line in Figure 3 meet) or through all of the points that define the convex hull (i.e, points where segments of the green line in Figure 3 meet).
I believe that all of the above methods will yield similar results except for small values of n, and I have thus chosen the first because it is the simplest.
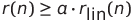, where _eq.png)
is the
piecewise-linear envelope of r(n) and a is a constant between 0
and 1.
I set the parameter a= 1 and generated a list of the first 30 highly-composite integers. The ith row of the table below contains the number i, the ith highly-composite number (n), r(n), the number of proper factors of n, and the factorization of n.
# of
i n r(n) proper factorization
factors
1 6 1.000 3 2 * 3
2 12 1.333 5 2^2 * 3
3 24 1.500 7 2^3 * 3
4 36 1.528 8 2^2 * 3^2
5 48 1.583 9 2^4 * 3
6 60 1.800 11 2^2 * 3 * 5
7 120 2.000 15 2^3 * 3 * 5
8 180 2.033 17 2^2 * 3^2 * 5
9 240 2.100 19 2^4 * 3 * 5
10 360 2.250 23 2^3 * 3^2 * 5
11 720 2.358 29 2^4 * 3^2 * 5
12 840 2.429 31 2^3 * 3 * 5 * 7
13 1260 2.467 35 2^2 * 3^2 * 5 * 7
14 1680 2.543 39 2^4 * 3 * 5 * 7
15 2520 2.714 47 2^3 * 3^2 * 5 * 7
16 5040 2.838 59 2^4 * 3^2 * 5 * 7
17 10080 2.900 71 2^5 * 3^2 * 5 * 7
18 15120 2.937 79 2^4 * 3^3 * 5 * 7
19 25200 2.966 89 2^4 * 3^2 * 5^2 * 7
20 27720 3.052 95 2^3 * 3^2 * 5 * 7 * 11
21 55440 3.187 119 2^4 * 3^2 * 5 * 7 * 11
22 110880 3.255 143 2^5 * 3^2 * 5 * 7 * 11
23 166320 3.294 159 2^4 * 3^3 * 5 * 7 * 11
24 277200 3.327 179 2^4 * 3^2 * 5^2 * 7 * 11
25 332640 3.364 191 2^5 * 3^3 * 5 * 7 * 11
26 554400 3.396 215 2^5 * 3^2 * 5^2 * 7 * 11
27 665280 3.398 223 2^6 * 3^3 * 5 * 7 * 11
28 720720 3.509 239 2^4 * 3^2 * 5 * 7 * 11 * 13
29 1441440 3.582 287 2^5 * 3^2 * 5 * 7 * 11 * 13
30 2162160 3.625 319 2^4 * 3^3 * 5 * 7 * 11 * 13
The above values of n are sometimes called superabundant integers.
Surprisingly, the number 30, which is the product of the first three primes, does not appear in the above list. One can obtain a more inclusive set of highly-composite integers by setting a= 0.9247. (I chose this value of a because it is the smallest that causes the number 30 to be classified as highly-composite). The first 100 such integers are shown in the table below.
# of
i n r(n) proper factorization
factors
1 6 1.000 3 2 * 3
2 12 1.333 5 2^2 * 3
3 24 1.500 7 2^3 * 3
4 30 1.400 7 2 * 3 * 5
5 36 1.528 8 2^2 * 3^2
6 48 1.583 9 2^4 * 3
7 60 1.800 11 2^2 * 3 * 5
8 72 1.708 11 2^3 * 3^2
9 120 2.000 15 2^3 * 3 * 5
10 180 2.033 17 2^2 * 3^2 * 5
11 240 2.100 19 2^4 * 3 * 5
12 360 2.250 23 2^3 * 3^2 * 5
13 420 2.200 23 2^2 * 3 * 5 * 7
14 480 2.150 23 2^5 * 3 * 5
15 720 2.358 29 2^4 * 3^2 * 5
16 840 2.429 31 2^3 * 3 * 5 * 7
17 1080 2.333 31 2^3 * 3^3 * 5
18 1260 2.467 35 2^2 * 3^2 * 5 * 7
19 1440 2.413 35 2^5 * 3^2 * 5
20 1680 2.543 39 2^4 * 3 * 5 * 7
21 2160 2.444 39 2^4 * 3^3 * 5
22 2520 2.714 47 2^3 * 3^2 * 5 * 7
23 3360 2.600 47 2^5 * 3 * 5 * 7
24 5040 2.838 59 2^4 * 3^2 * 5 * 7
25 7560 2.810 63 2^3 * 3^3 * 5 * 7
26 7920 2.664 59 2^4 * 3^2 * 5 * 11
27 9240 2.740 63 2^3 * 3 * 5 * 7 * 11
28 10080 2.900 71 2^5 * 3^2 * 5 * 7
29 10920 2.692 63 2^3 * 3 * 5 * 7 * 13
30 12600 2.838 71 2^3 * 3^2 * 5^2 * 7
31 13860 2.782 71 2^2 * 3^2 * 5 * 7 * 11
32 15120 2.937 79 2^4 * 3^3 * 5 * 7
33 15840 2.723 71 2^5 * 3^2 * 5 * 11
34 16380 2.733 71 2^2 * 3^2 * 5 * 7 * 13
35 16800 2.720 71 2^5 * 3 * 5^2 * 7
36 17640 2.781 71 2^3 * 3^2 * 5 * 7^2
37 18480 2.865 79 2^4 * 3 * 5 * 7 * 11
38 20160 2.931 83 2^6 * 3^2 * 5 * 7
39 21840 2.815 79 2^4 * 3 * 5 * 7 * 13
40 22680 2.841 79 2^3 * 3^4 * 5 * 7
41 23760 2.758 79 2^4 * 3^3 * 5 * 11
42 25200 2.966 89 2^4 * 3^2 * 5^2 * 7
43 27720 3.052 95 2^3 * 3^2 * 5 * 7 * 11
44 30240 3.000 95 2^5 * 3^3 * 5 * 7
45 32760 3.000 95 2^3 * 3^2 * 5 * 7 * 13
46 35280 2.907 89 2^4 * 3^2 * 5 * 7^2
47 36960 2.927 95 2^5 * 3 * 5 * 7 * 11
48 37800 2.937 95 2^3 * 3^3 * 5^2 * 7
49 40320 2.946 95 2^7 * 3^2 * 5 * 7
50 42840 2.933 95 2^3 * 3^2 * 5 * 7 * 17
51 45360 2.969 99 2^4 * 3^4 * 5 * 7
52 50400 3.030 107 2^5 * 3^2 * 5^2 * 7
53 55440 3.187 119 2^4 * 3^2 * 5 * 7 * 11
54 60480 3.032 111 2^6 * 3^3 * 5 * 7
55 65520 3.133 119 2^4 * 3^2 * 5 * 7 * 13
56 70560 2.970 107 2^5 * 3^2 * 5 * 7^2
57 75600 3.068 119 2^4 * 3^3 * 5^2 * 7
58 83160 3.156 127 2^3 * 3^3 * 5 * 7 * 11
59 85680 3.064 119 2^4 * 3^2 * 5 * 7 * 17
60 90720 3.033 119 2^5 * 3^4 * 5 * 7
61 92400 2.994 119 2^4 * 3 * 5^2 * 7 * 11
62 95760 3.040 119 2^4 * 3^2 * 5 * 7 * 19
63 98280 3.103 127 2^3 * 3^3 * 5 * 7 * 13
64 100800 3.062 125 2^6 * 3^2 * 5^2 * 7
65 105840 3.007 119 2^4 * 3^3 * 5 * 7^2
66 110880 3.255 143 2^5 * 3^2 * 5 * 7 * 11
67 120120 3.028 127 2^3 * 3 * 5 * 7 * 11 * 13
68 120960 3.048 127 2^7 * 3^3 * 5 * 7
69 128520 3.034 127 2^3 * 3^3 * 5 * 7 * 17
70 131040 3.200 143 2^5 * 3^2 * 5 * 7 * 13
71 138600 3.187 143 2^3 * 3^2 * 5^2 * 7 * 11
72 151200 3.133 143 2^5 * 3^3 * 5^2 * 7
73 163800 3.133 143 2^3 * 3^2 * 5^2 * 7 * 13
74 166320 3.294 159 2^4 * 3^3 * 5 * 7 * 11
75 171360 3.129 143 2^5 * 3^2 * 5 * 7 * 17
76 180180 3.073 143 2^2 * 3^2 * 5 * 7 * 11 * 13
77 181440 3.065 139 2^6 * 3^4 * 5 * 7
78 184800 3.058 143 2^5 * 3 * 5^2 * 7 * 11
79 191520 3.105 143 2^5 * 3^2 * 5 * 7 * 19
80 194040 3.124 143 2^3 * 3^2 * 5 * 7^2 * 11
81 196560 3.239 159 2^4 * 3^3 * 5 * 7 * 13
82 201600 3.078 143 2^7 * 3^2 * 5^2 * 7
83 211680 3.071 143 2^5 * 3^3 * 5 * 7^2
84 214200 3.064 143 2^3 * 3^2 * 5^2 * 7 * 17
85 221760 3.288 167 2^6 * 3^2 * 5 * 7 * 11
86 226800 3.102 149 2^4 * 3^4 * 5^2 * 7
87 229320 3.071 143 2^3 * 3^2 * 5 * 7^2 * 13
88 231840 3.070 143 2^5 * 3^2 * 5 * 7 * 23
89 240240 3.162 159 2^4 * 3 * 5 * 7 * 11 * 13
90 249480 3.190 159 2^3 * 3^4 * 5 * 7 * 11
91 257040 3.168 159 2^4 * 3^3 * 5 * 7 * 17
92 262080 3.233 167 2^6 * 3^2 * 5 * 7 * 13
93 277200 3.327 179 2^4 * 3^2 * 5^2 * 7 * 11
94 287280 3.144 159 2^4 * 3^3 * 5 * 7 * 19
95 294840 3.137 159 2^3 * 3^4 * 5 * 7 * 13
96 302400 3.166 167 2^6 * 3^3 * 5^2 * 7
97 327600 3.271 179 2^4 * 3^2 * 5^2 * 7 * 13
98 332640 3.364 191 2^5 * 3^3 * 5 * 7 * 11
99 342720 3.162 167 2^6 * 3^2 * 5 * 7 * 17
100 360360 3.364 191 2^3 * 3^2 * 5 * 7 * 11 * 13
Note that powers of prime numbers do not appear in the above tables because such numbers have few factors. Starting with the number 120, all highly-composite numbers are multiples of 60.
In Figure 4 below, I've plotted the normalized sum of the proper factors of
n versus n, with a logarithmic x-axis, and with color coding to
indicate prime numbers (blue),
perfect numbers
(yellow), powers of 10 (green), highly-composite numbers (red), and all other
numbers (gray).
As we can see from the figure, highly-composite numbers are much less
plentiful than prime numbers, but more plentiful than powers of 10. According
to the Prime Number
Theorem, the number of primes in {1, 2, ..., N} tends to
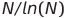in the limit as N goes to infinity. Note that the
number of highly-composite numbers per decade (interval between one power of 10
and the next) appears to be slowly growing. I suspect that the number of
highly-composite integers in {1, 2, ..., N} tends to
 ln(ln(N))_eq.png)
in the limit of large N, but have not
proven this.
Note that powers of 10 fall midway between prime numbers and highly-composite numbers on the figure. I love the simplicity of the metric system and believe that the U.S. should have made the switch to metric decades ago, but highly-composite numbers have a certain attraction and are more convenient than powers of 10 in some situations.
All of the numerical results presented here, including the graphs, were
generated using the Python module primes.py. This Python module
contains functions for performing various calculations involving prime numbers,
including primality testing, prime factorization, and the like. The following
functions are particularly relevant to this article:
sum_of_proper_factors calculates the sum of the proper
factors of the given integer. This function was developed in collaboration with
Benjamin L. Cosman. [Ben—one of my nephews—recently completed his
undergraduate studies at the California Institute of Technology.]
print_highly_composite generated the two tables.
find_highly_composite returns a list of highly-composite
integers and a list containing the corresponding values of r(n).
print_composite calculates the specified number of
highly-composite integers (see the above definition) and displays a table of
highly-composite integers and the corresponding values of the above ratio.