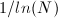 in the limit of large N. [ln(N) is the natural logarithm of N.]
in the limit of large N. [ln(N) is the natural logarithm of N.]


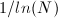 in the limit of large N. [ln(N) is the natural logarithm of N.]
in the limit of large N. [ln(N) is the natural logarithm of N.]
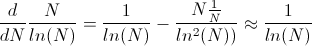 for large N. Vicinity is a
bit vague and not easily clarified. Suffice it to say that the interval over
which we examine the average spacing must be large compared to the average
spacing (to eliminate small sample variation) but still small compared to
N.
for large N. Vicinity is a
bit vague and not easily clarified. Suffice it to say that the interval over
which we examine the average spacing must be large compared to the average
spacing (to eliminate small sample variation) but still small compared to
N.
from numpy import * from primes import * P= array(find_primes(200)) ((980<=P) & (P<=1020)).sum()The interpreter should display a result of 6. Not bad! Actually, predictions of the number of primes to be found in a short interval are typically not this accurate because the distribution of primes is highly irregular.
Note that (3, 5, 7) is the only prime triple of the form (p, p+2, p+4) because in any such triple, at least one of the three numbers must be divisible by 3. The following table lists the first 20 and selected larger prime triples (large integers are written without commas so that the rate of growth can be judged from the lengths of the numbers):
1: 2 3 5
2: 3 5 7
3: 5 7 11
4: 7 11 13
5: 11 13 17
6: 13 17 19
7: 17 19 23
8: 37 41 43
9: 41 43 47
10: 67 71 73
11: 97 101 103
12: 101 103 107
13: 103 107 109
14: 107 109 113
15: 191 193 197
16: 193 197 199
17: 223 227 229
18: 227 229 233
19: 277 281 283
20: 307 311 313
100: 7873 7877 7879
1000: 247603 247607 247609
10000: 5037913 5037917 5037919
100000: 88011613 88011617 88011619
1000000: 1385338061 1385338063 1385338067
Strictly speaking, the numbers of primes, primes pairs, and prime triples are all the same because all are countably infinite. (A set is countably infinite if there is a one-to-one mapping between its elements and the integers; see the Wikipedia article referenced below for further discussion). But, in another sense, there are far more primes than prime pairs, and far more prime pairs than prime triples. The 3 millionth prime number is 49,979,687; comparing this with the millionth prime triple in the above table, we can see that only a tiny percentage of the primes between 1 and 1,385,338,067 occur in prime triples.
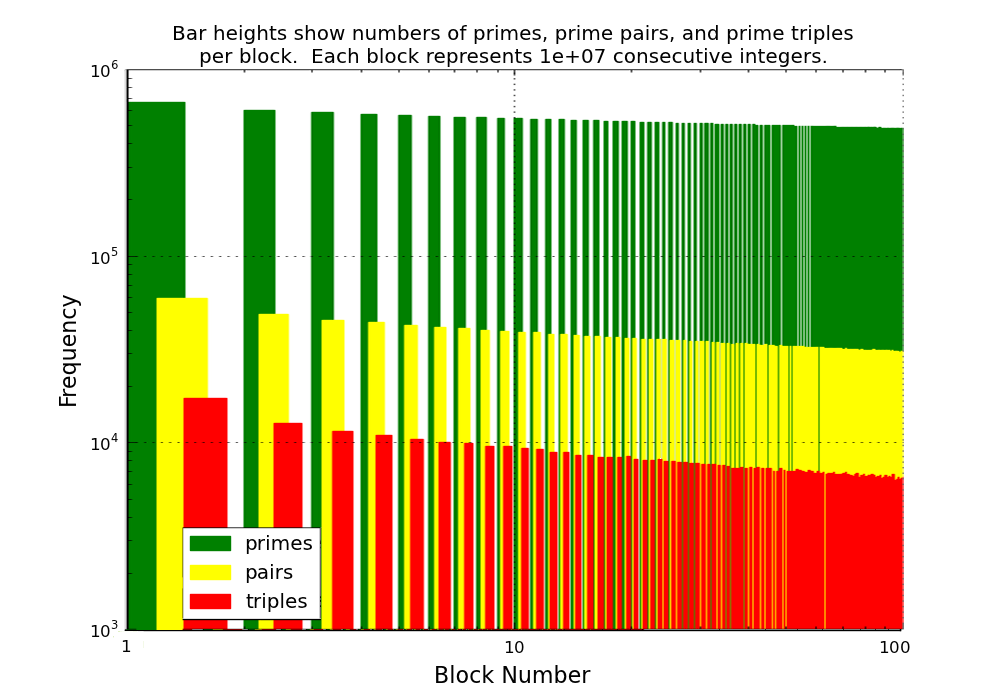
Figure 1 below displays the frequencies of primes, primes pairs, and prime
triples among the first billion integers. Each set of three bars represents the
counts from a block of 10 million consecutive integers. Note that the frequency
of primes pairs diminishes faster than that of primes, while the frequency of
prime triples diminishes even faster. (The y-axis has a logarithmic scale, so
the increasing distances between the tops of the yellow and green bars and
between the red and yellow bars indicates that the ratios are increasing). Thus,
the tendency of prime numbers to cluster together gradually diminishes, i.e.,
the primes become increasingly isolated.
The next several plots are histograms of counts of prime numbers from equal-sized blocks of consecutive integers. (Each plot was generated using equal-sized blocks, but the block size is differs from one plot to the next, as noted in the plot titles). A new block starts whenever an integer n is reached such that n mod b= 1, where b is the block size. In each plot, the green bars show the counts of prime numbers, while the blue bars show the corresponding Poisson probability mass function (PMF). The mean of the Poisson distribution has been chosen to match the sample mean of the data. (The scaling makes the two sets of bars have the same total area).
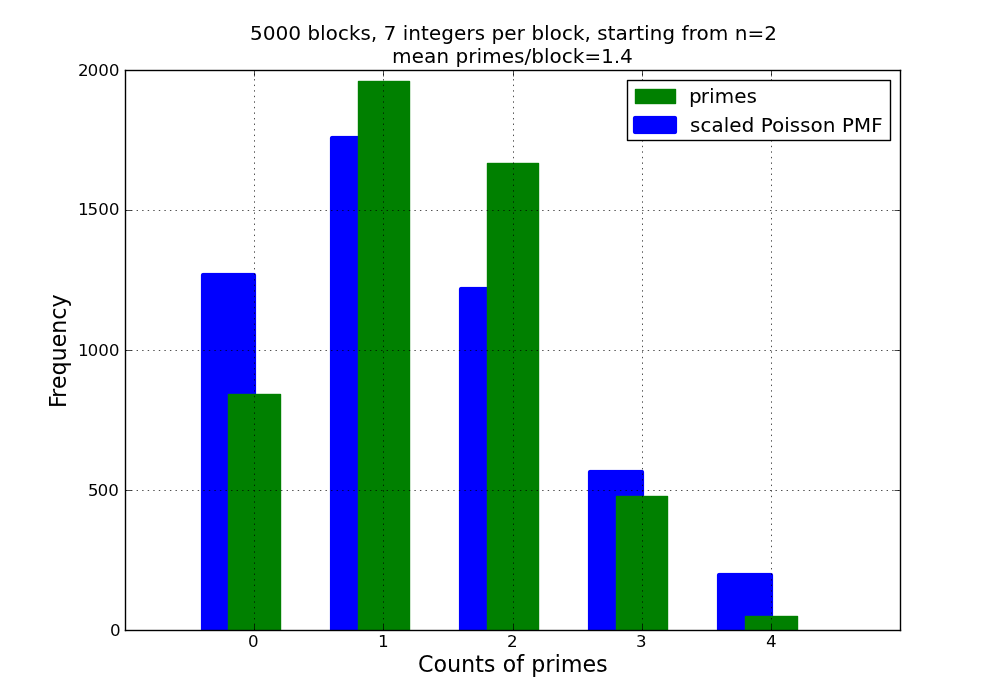
Figure 2 was generated with a block size b= 7 and initial integer n=2. (This
block size was chosen to produce a mean number of primes per block between 1 and
2). Despite the ample size of the sample, the Poisson distribution does not
appear to be a good fit to the data.
The data for Figure 3 was generated by increasing the block size, which
increases the mean of the Poisson distribution. Notice that the distribution is
beginning to converge to the normal curve. (Recall that the Poisson tends to a
normal limit as its mean becomes large).
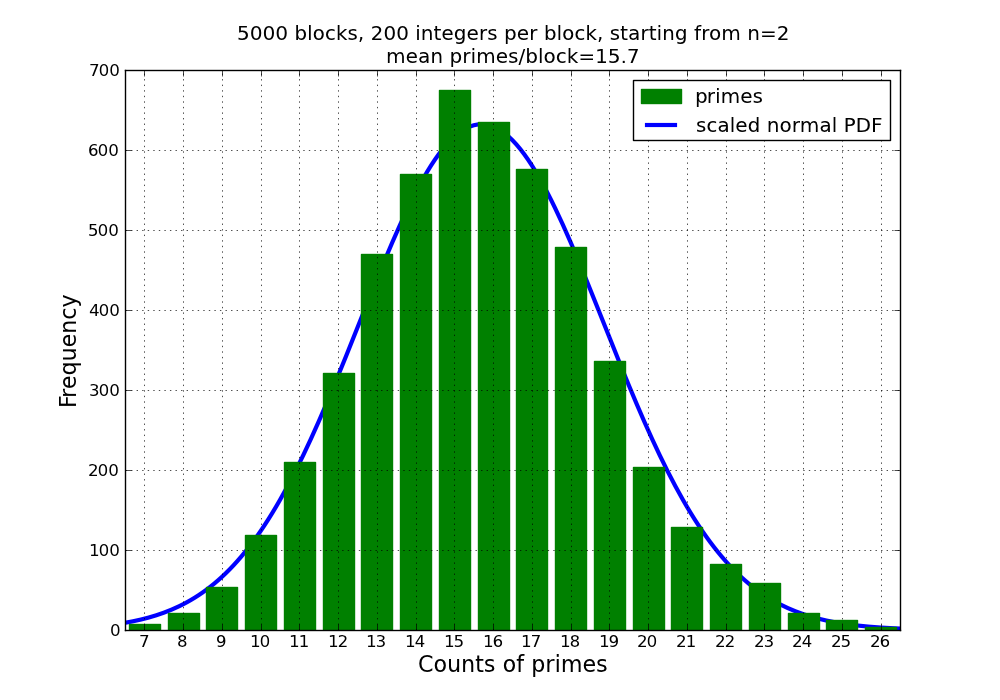
Figure 4 was created by specifying a value of 22000 for the initial integer.
This value was chosen to produce an average spacing of 10 between consecutive
prime numbers. Note that the fit between the data and the Poisson distribution
is no better than what was obtained with an initial integer of 2.
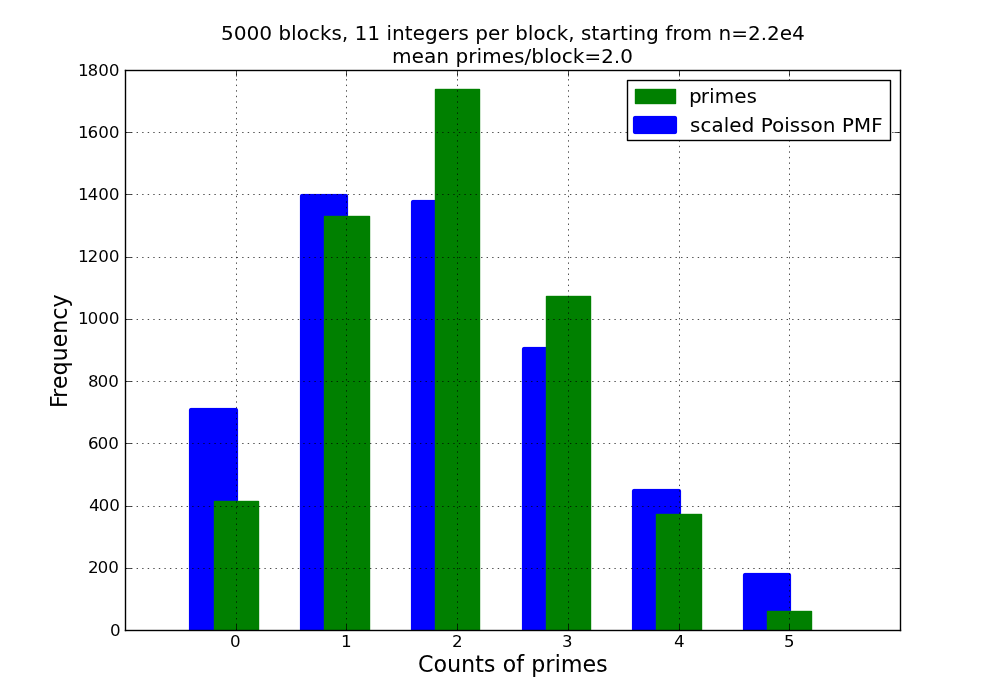
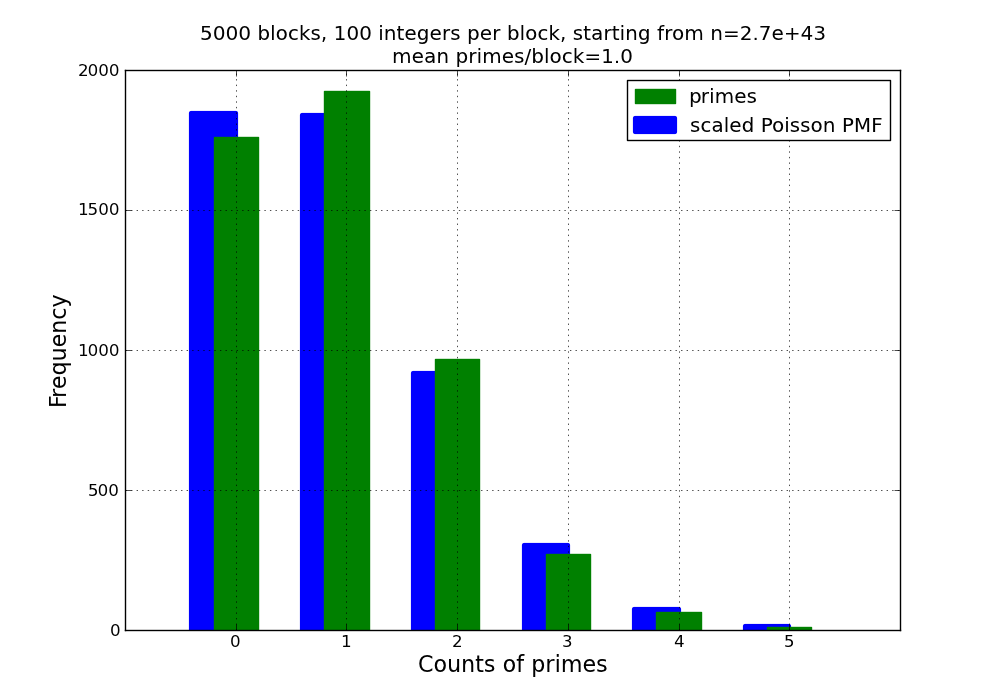
Figure 5 was created by specifying a value of 2.7e43 for the initial integer.
This value was chosen to produce an average spacing of 100 between consecutive
prime numbers. Note that we have finally obtained a reasonably close fit
between the data and the Poisson distribution.
The above statistical results suggest two questions:
Why does the prime number sequence exhibit Poisson behavior? The proof of this requires some difficult math; I hope to eventually add a discussion of some of the ideas in the proof to this web page.
Why does the Poisson behavior emerge only for relatively large integers? Aside from small-sample variation, I believe that there are two explanations for discrepancies between the histograms and the scaled Poisson distribution:
The underlying distribution of the data is shifting from one block to the next as the frequency of primes diminishes. For any fixed block size, we can see from the Prime Number Theorem that this change should be initially rapid, but gradually slowing.
For small integers, the discrete step between one integer and the next is significant compared to the average increment between one prime number and the next. In a Poisson process, the time between one 'arrival' and the next must be an exponential random variable, which has a continuous distribution, and thus cannot be constrained to the integers.
For both radioactive decay and prime numbers, the expected (average) number of
'events' per unit time diminishes, and both processes are thus non-stationary.
The rate laws are of course different. The rate of radioactive decay diminishes
exponentially (hence the term half life), while the rate at which prime
numbers appear decays much more slowly (see the discussion of the Prime Number
Theorem above). This difference is important: If one is willing to wait long
enough (long enough might make the present age of the universe seem
insignificant) any chunk of radioactive material will eventually emit its last
particle. The prime numbers, on the other hand, go on forever.
(1) Mathworld article on twin primes
(2) This Wikipedia article defines the term 'countably infinite'.
(3) primes.py: This Python module contains functions for
performing various calculations involving prime numbers, including primality
testing, prime factorization, and the like. All numerical results presented in
this article were generated using the Enthought Python distribution and the
primes.py module.
Last update: 16 May, 2020